Self Attention
- 예제
- code
- 참고

Self Attention

Self-attention은

하나의 sequence 안에서 각 token이
같은 sequence에 속한 모든 token들과의 관련성(attention score)을 고려하여
자신의 representation(표현, dense vector)을 계산하는 메커니즘이다.

각 token은 query, key, value로 변환(linear transform)되며,

token 간의 관련성은 scaled dot-product 방식으로
$q \cdot k / \sqrt{d_k}$를 계산한 뒤 softmax로 정규화.
- scaled ($1/\sqrt{d_k}$) 는
  - embedding의 크기 $d_k$가 커질 경우, dot product의 값이 커지게 되어
  - softmax 처리시 특정 token에 지나치게 큰 attention이 집중되고
  - 이로 인해 학습시 gradient 가 불안정해지는 것을 방지해줌
  - 이 것이 scaled dot-product 라는 이름에서 scaled 에 해당함.
- Normal distribution 을 따르는 component 로 구성된 벡터 2개의 dot-product는 평균이 0, 분산이 차원수 임: 때문에 std 는 차원수의 square root이며, 이를 scale 로 삼음.

이 과정을 통해 sequence 내에서 중요한 token에는 더 큰 가중치(attention weight)가 부여되고, context(문맥)을 반영한 token representation 이 생성됨.

attention weight는 attention score를 softmax 처리하여 확률로 만든 것임.

ref: Hanus Kim's blog

\[\mathrm{Attention}(Q, K, V) = \mathrm{softmax}\!\left(\frac{QK^{\top}}{\sqrt{d_k}}\right)V\]

$Q \in \mathbb{R}^{T_q \times d_k}$ 는 쿼리 벡터들을 행 단위로 쌓아 구성한 행렬이며, $T_q$는 쿼리의 개수, 즉 쿼리 시퀀스의 길이를 의미한다.
$K \in \mathbb{R}^{T_k \times d_k}$ 는 키 벡터들을 행 단위로 쌓아 구성한 행렬이며, $T_k$는 각 쿼리가 참조할 수 있는 위치의 개수, 즉 참조 대상이 되는 시퀀스의 길이를 의미한다.
$V \in \mathbb{R}^{T_k \times d_v}$ 는 값 벡터들을 행 단위로 쌓아 구성한 행렬이며, 키와 동일하게 $T_k$개의 원소를 가진다.
$d_k$는 쿼리와 키 벡터의 차원, $d_v$는 값 벡터의 차원을 의미한다.

실제로, 각 token은 적절한 key, query, value가 되도록 trainable parameter인 $W^Q, W^k, W^V$를 통한 linear transform (로 다른 역할의 표현 공간으로 projection)을 함. 입력이 $X$ 일때 $Q,K,V$는 다음과 같음:

$Q =X W^Q $
$K =X W^K $
$V =X W^V $

입력 $X \in \mathbb{R}^{T \times d_{\text{model}}} $는

$ W^Q, W^K, W^V $를 통해 각각 다음의 공간으로 사상(projection)시킴
- $Q \in \mathbb{R}^{T \times d_k}$ ("이 토큰이 무엇을 찾는가"를 표현하는 공간),
- $K \in \mathbb{R}^{T \times d_k}$ ("이 토큰이 어떤 기준으로 참조되는가"를 표현하는 공간,
- $V \in \mathbb{R}^{T \times d_v}$ ("실제로 전달할 정보 내용")
이 분리를 통해 Transformer는 token 간 관계를 학습 가능한 방식으로 모델링.
이는 여러 관계를 학습하기 위해 보고자 하는 관계의 숫자만큼 head ($h$개)를 도입한 multi-head attention에서 사용됨:
- $d_q = d_k = d_k = d_{model}/h$ 가 성립.
- $d_q$ 는 $d_k$ 와 inner product를 하므로 같아야 함 (다르면 linear transform으로 같도록 처리).
- $h$ : head의 수.

Scaled Dot-Product Attention의 경우와 Multi-Head Attention의 차이는 token의 embedding을 모두 다 사용하여 하나의 관계에 대한 attention을 만드느냐, embedding을 head의 갯수로 나누어 이 작은 token의 일부로 하나씩의 관계에 대한 attention을 만드느냐의 차이임.

또한 $\mathrm{softmax}(\cdot)$ 함수는 각 Query에 대해 Key 차원 방향으로 적용되어, 어텐션 가중치의 합이 1이 되도록 정규화한다.

ref: Self-Attention. Ramendra Kumar

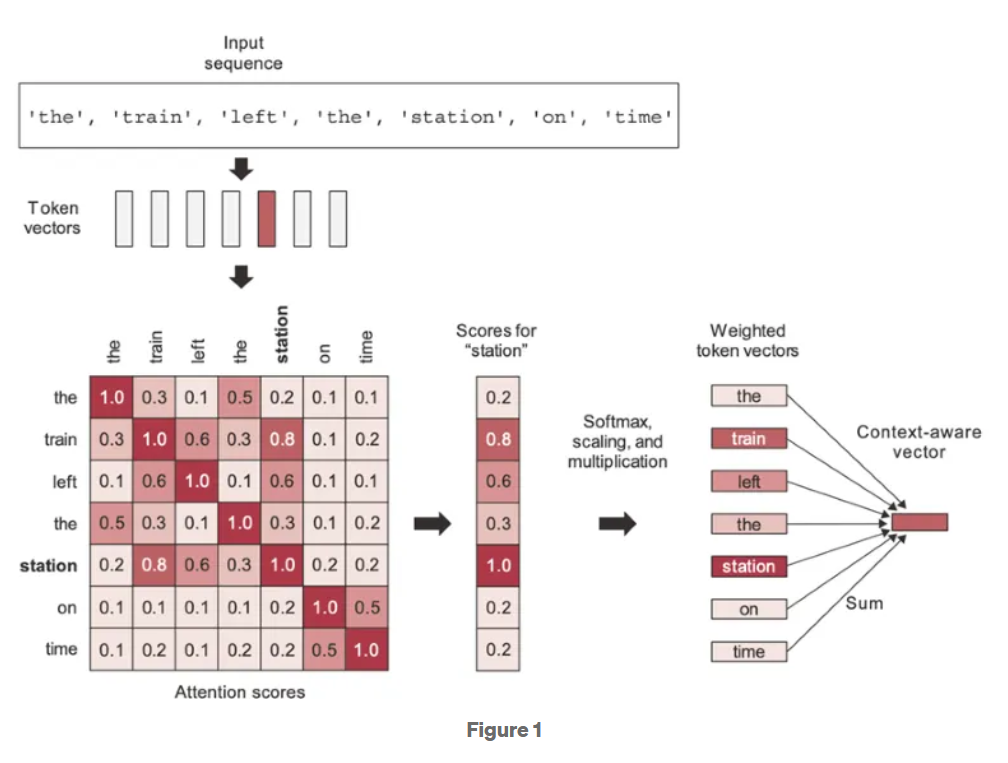
다음 그림이 Transformer에서의 Self Attention을 구하기 위한 scaled dot product의 computational graph임.

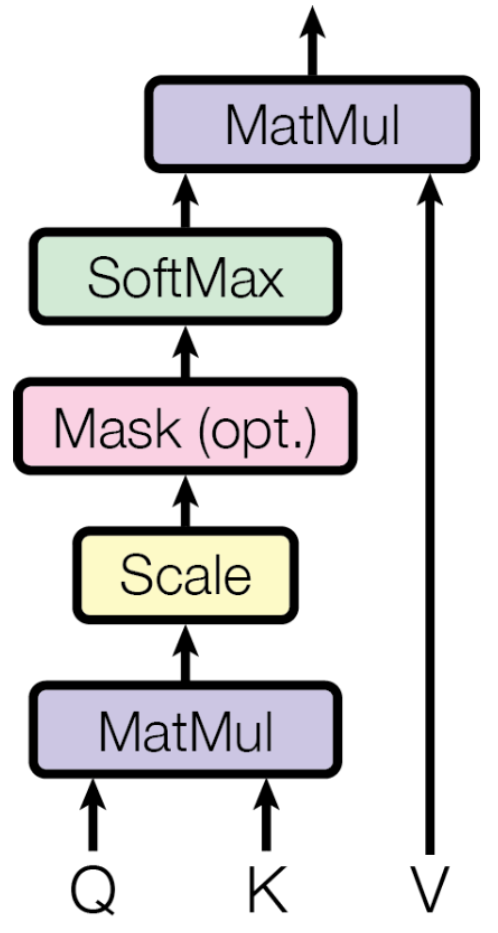
original: Attention is All You Need, 2017

예제

"Time flies like an arrow" 라는 sentense의 self attention 을 구하여 시각화 한 예임.

flies 가 파리들, 날다 의 뜻을 가질 수 있는데
위의 경우 날다 이므로 "arrow"와 매우 큰 관계를 가짐을 확인할 수 있음.

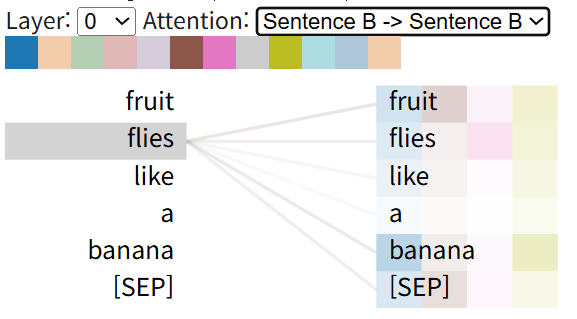
"Fruit flies likes a banana" 의 sentense의 예는 다음과 같음:

code

    def scaled_dot_product_attention(
        self, 
        Q: torch.Tensor, 
        K: torch.Tensor, 
        V: torch.Tensor,
        mask: Optional[torch.Tensor] = None
    ) -> torch.Tensor:
        """
        scaled dot-prodcut attention 어텐션 계산
        
        Attention(Q, K, V) = softmax(QK^T / sqrt(d_k))V
        
        Args:
            Q: Query (batch_size, num_heads, seq_len, d_k)
            K: Key (batch_size, num_heads, seq_len, d_k)
            V: Value (batch_size, num_heads, seq_len, d_k)
            mask: 마스크 (batch_size, 1, seq_len, seq_len) or (batch_size, 1, 1, seq_len)
        Returns:
            어텐션 출력 (batch_size, num_heads, seq_len, d_k)
        """
        # QK^T / sqrt(d_k)
        scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
        
        # 마스크 적용 (필요한 경우)
        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))
        
        # Softmax 적용
        attention_weights = F.softmax(scores, dim=-1)
        attention_weights = self.dropout(attention_weights)
        
        # Value와 곱하기
        output = torch.matmul(attention_weights, V)
        
        return output

Self Attention

예제

code

참고